ChaCha20-Poly1305 and Nonce reuse attack

Background

When doing picoCTF 2025, I encountered a challenge that requires to forge a TAG for a AEAD cipher ChaCha20-Poly1305 with a reused key and nonce. This post is a summary of the cipher and the attack.

ChaCha20-Poly1305

Like AES-GCM, ChaCha20-Poly1305 have two components: a encryption cipher and a tag generation part.

ChaCha20

ChaCha20 can be understood as a 20 rounds (80 quarter rounds) variant of ChaCha cipher - a stream cipher. It takes a 256-bit key, a 96-bit nonce, and a 32-bit counter to generate a keystream. The keystream is then xored with the plaintext to produce the ciphertext.

Internal

Quarter Round is the basic of Chacha cipher, which operate on 4 32-bit unsigned integers $a, b, c, d$ as follows, and denote as QUARTERROUND(a,b,c,d)

1
2
3
4

   a += b; d ^= a; d = d << 16;
   c += d; b ^= c; b = b << 12;
   a += b; d ^= a; d = d << 8;
   c += d; b ^= c; b = b << 7;

A state of ChaCha20 can be represented as 4x4 matrix of 32-bit unsigned integers.

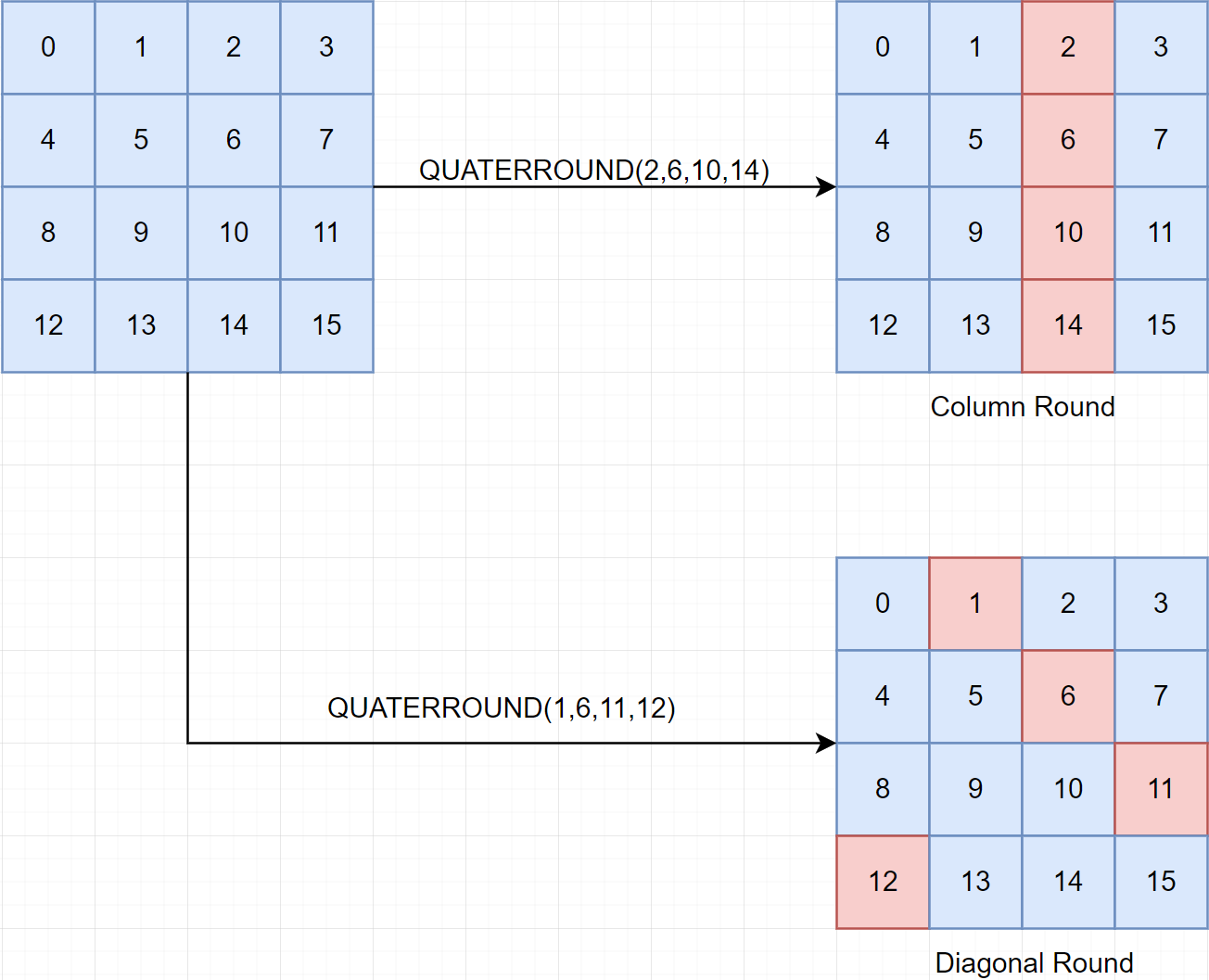
ChaCha20 runs 20 rounds with alternating between column rounds and diagonal rounds. Below present of 2 rounds. So it will run 10 iterations for the list of rounds below.

   inner_block (state):
      QUARTERROUND(state, 0, 4, 8,12)
      QUARTERROUND(state, 1, 5, 9,13)
      QUARTERROUND(state, 2, 6,10,14)
      QUARTERROUND(state, 3, 7,11,15)
      QUARTERROUND(state, 0, 5,10,15)
      QUARTERROUND(state, 1, 6,11,12)
      QUARTERROUND(state, 2, 7, 8,13)
      QUARTERROUND(state, 3, 4, 9,14)
   end

   chacha20_block(key, counter, nonce):
      state = constants | key | counter | nonce
      working_state = state
      for i=1 upto 10
         inner_block(working_state)
         end
      state += working_state
      return serialize(state)
   end

Encryption

Because ChaCha20 is a stream cipher decryption is the same as encryption.

• Input:
  • Key: 256-bit key.
  • Nonce: 96-bit nonce.
  • Counter $(J)$: 32-bit counter. In ChaCha20-Poly1305, the counter is set to 1 because block 0 is used to derive $(r,s)$ for Poly1305.
  • Plaintext: arbitrary length plaintext.
• Output:
  • Ciphertext: same length as plaintext.

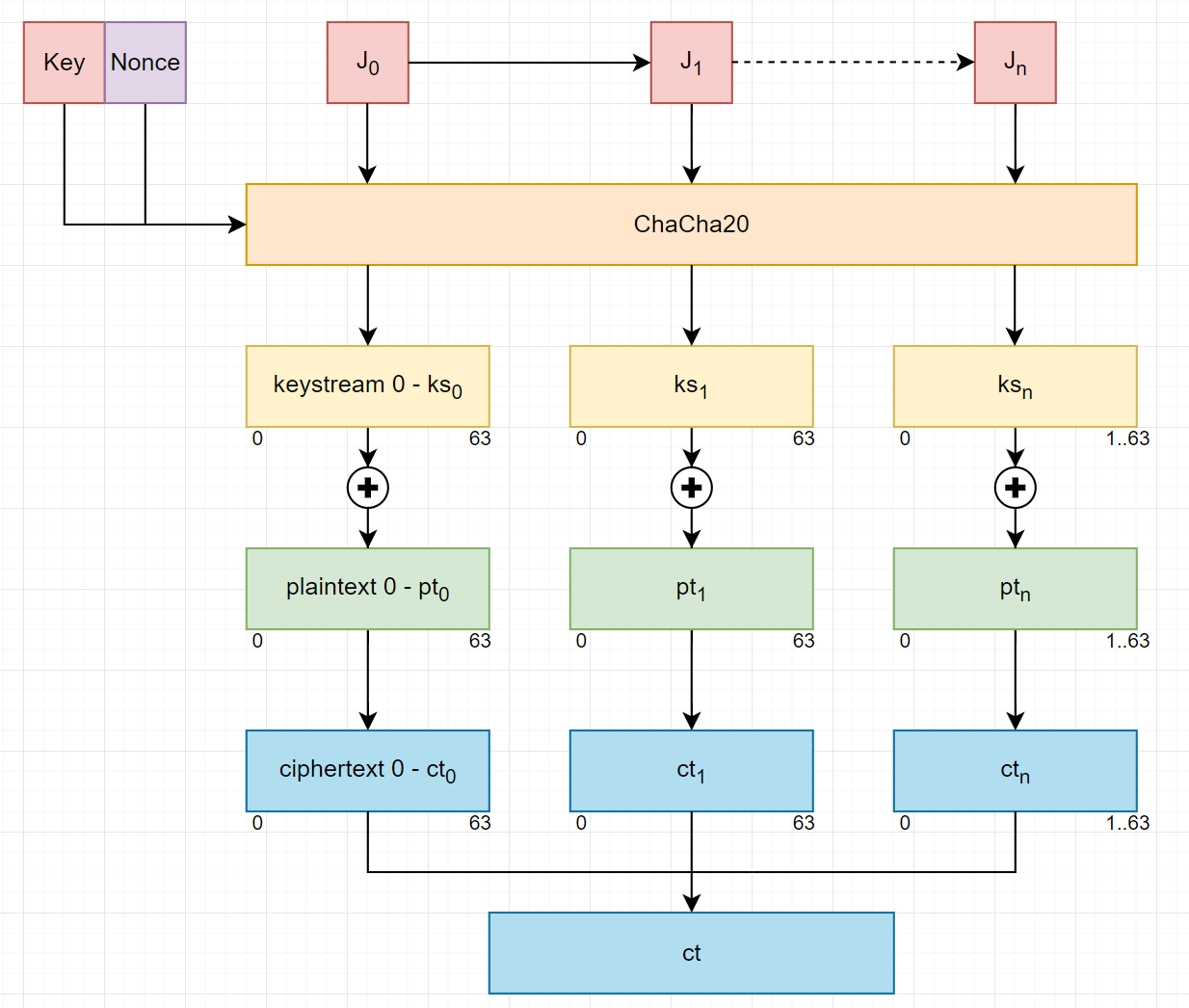
Note: all number in figure are for (0 .. 63) bytes = 512 bits.

• In pesudo code:

   chacha20_encrypt(key, counter, nonce, plaintext):
      for j = 0 upto floor(len(plaintext)/64)-1
         key_stream = chacha20_block(key, counter+j, nonce)
         block = plaintext[(j*64)..(j*64+63)]
         encrypted_message +=  block ^ key_stream
         end
      if ((len(plaintext) % 64) != 0)
         j = floor(len(plaintext)/64)
         key_stream = chacha20_block(key, counter+j, nonce)
         block = plaintext[(j*64)..len(plaintext)-1]
         encrypted_message += (block^key_stream)[0..len(plaintext)%64]
         end
      return encrypted_message
      end

Poly1305

The original Poly1305 first appear in The Poly1305-AES message-authentication code. Briefly, It a MAC function requires 2 128-bits keys, and 1 128-bits nonce. AES used 1 key to encrypt nonce and compile with another key to have a pair $(r,s)$.

The pair $(r,s)$ must be unpredictable and follow the standard below. Here $r$ is treated as 16-octet little-endian number because of $C$ limitation.

• r[3], r[7], r[11], and r[15] are required to have their top four bits clear (be smaller than 16)

• r[4], r[8], and r[12] are required to have their bottom two bits clear (be divisible by 4)

And the Poly1305 function is as follow, because $msg$ when going into poly1305 have been padded to a multiple of 16 bytes so we don’t consider last block < 16 bytes.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

def poly1305(r,s,msg):
    def clamp(r):
        r &= 0x0ffffffc0ffffffc0ffffffc0fffffff
        return r
    a = 0
    r = clamp(r)
    p = (1<<130)-5
    for i in range(0,len(msg),16):
        block = msg[i:i+16]
        assert len(block) == 16
        n = le_bytes_to_num(block + b'\x01')
        a+=n
        a = (r*a)%p
    a+=s
    return (a % (1 << 128)).to_bytes(16,'little')

So the Poly1305 function can be written as

$$\operatorname{Poly1305}(r, s, \mathrm{msg}) = \left(\left(\mathrm{block}_1 r^i + \mathrm{block}_2 r^{i-1} + \dots + \mathrm{block}_i r^1\right) \bmod (2^{130} - 5) + s\right) \bmod 2^{128}$$

$(r,s)$ pair generation for ChaCha20 is simple as follow.

1
2
3
4

def poly1305_key_gen(key,nonce):
    cipher  = ChaCha20.new(key=key, nonce=nonce)
    ks = cipher.encrypt(b'\x00'*32)
    return ks[:16],ks[16:] #(r,s) in bytes -> need to convert to le int

ChaCha20-Poly1305 encryption/decryption.

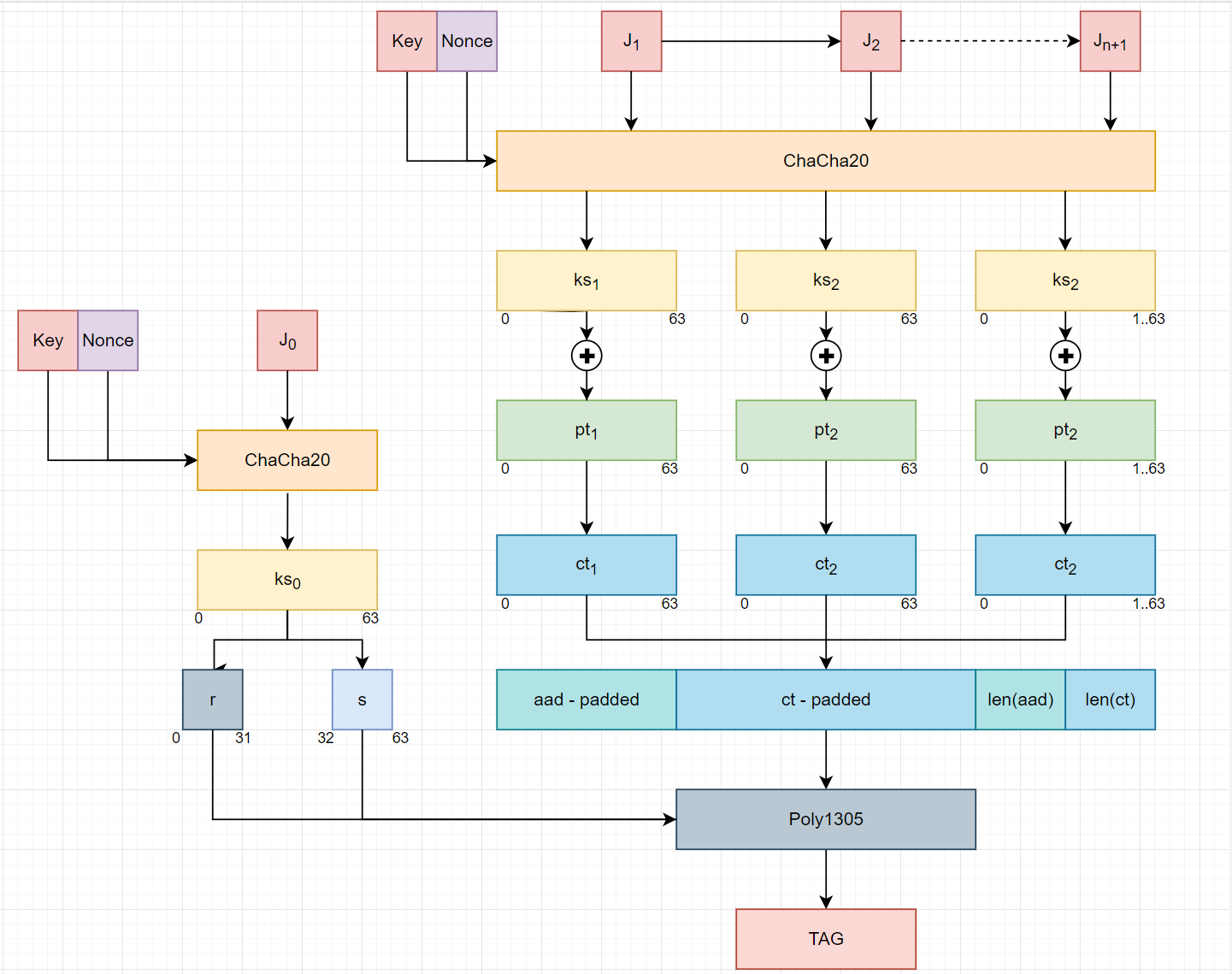
Here is sanity check script.

Reuse Nonce attack:

In Oracle scheme, The key is often reused for multiple messages, but when Nonce is reused, we will have 2 $ct$ and $tag$ pairs from the same $(r,s)$ pairs

$$tag_1 = Poly1305(r, s, pad(ct_1)) = ((block_{1,1} r^i + block_{1,2} r^{i-1} + \dots + block_{1,i} r^1) \bmod (2^{130} - 5) + s) \bmod 2^{128}$$ $$tag_2 = Poly1305(r, s, pad(ct_2)) = ((block_{2,1} r^i + block_{2,2} r^{i-1} + \dots + block_{2,i} r^1) \bmod (2^{130} - 5) + s) \bmod 2^{128}$$ $$tag_1 - tag_2 = (r^i A_1 + r^{i-1} A_2 + \dots + r^1 A_i) \bmod (2^{130} - 5) \bmod 2^{128},\quad A_i = block_{1,i} - block_{2,i}$$ $$tag_1 - tag_2 = (r^i A_1 + r^{i-1} A_2 + \dots + r^1 A_i) + k 2^{128} \bmod (2^{130} - 5),\quad k \in \{-4, 4\}$$

From this we can recover $r$ easily and check if $r$ is correct by using clamp function and derive $s$ from $tag_1$ and $tag_2$ and check if equal. From $r,s$ we can forge a tag for any message using the keystream generated from ChaCha20.

Example.

Challenge ChaCha Slide in picoCTF 2025: We are given 2 pair (ct,tag) - known plaintext to get the keystream, and we need to forge a tag for a new message.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101

from pwn import *
from sage.all import *

def le_to_little_endian_pad(length: int) -> str:
    return length.to_bytes(8, 'little')

def le_bytes_to_num(b: bytes) -> int:
    return int.from_bytes(b, 'little')

def pad_to_16(data: bytes) -> bytes:
    if data == b'':
        return b''
    return data + b'\x00'*(16-len(data)%16)
def padding(data: bytes,aad: bytes) -> bytes:
    return pad_to_16(aad) + pad_to_16(data) +le_to_little_endian_pad(len(aad))+le_to_little_endian_pad(len(data))

def clamp(r):
        r &= 0x0ffffffc0ffffffc0ffffffc0fffffff
        return r
def poly1305_symbolic(r,s,data):
    a = 0
    for i in range(0,len(data),16):
        block = data[i:i+16]
        n = le_bytes_to_num(block + b'\x01')
        a+=n
        a = (r*a)
    a+=s
    return a
def poly1305_normal(r,s,data):
    a = 0
    p = (1<<130)-5
    for i in range(0,len(data),16):
        block = data[i:i+16]
        n = le_bytes_to_num(block + b'\x01')
        a+=n
        a = (r*a)%p
    a+=s
    return a

io = process(['python3', 'challenge.py'])
io.recvuntil(b'(hex):')
pt1 = bytes.fromhex(io.recvline().strip().decode())
io.recvuntil(b'(hex):')
ct1 = bytes.fromhex(io.recvline().strip().decode())
io.recvuntil(b'(hex):')
pt2 = bytes.fromhex(io.recvline().strip().decode())
io.recvuntil(b'(hex):')
ct2 = bytes.fromhex(io.recvline().strip().decode())


ciphertext1 = ct1[:-28]
tag1 = ct1[-28:-12]
nonce1 = ct1[-12:]
ciphertext2 = ct2[:-28]
tag2 = ct2[-28:-12]
nonce2 = ct2[-12:]
assert nonce1 == nonce2


C1 = padding(ciphertext1,b'')
C2 = padding(ciphertext2,b'')
p = 2**130 - 5
K = Zmod(p)
PR = PolynomialRing(K, 'r')
r = PR.gen()
T1 = le_bytes_to_num(tag1)
T2 = le_bytes_to_num(tag2)

x1 = poly1305_symbolic(r, 0, C1)
x2 = poly1305_symbolic(r, 0, C2)
res = []
f = (x1-x2)
for k in range(-4,4):
    A = T1-T2+k*2**128
    f_ = A-f
    for r,_ in f_.roots():
        if clamp(int(r)) == int(r):
            s = (T1 - int(x1(r))) % 2**128
            s2 = (T2 - int(x2(r))) % 2**128
            if s == s2:
                res.append((int(r),s))
            
r,s = res[0]
# sanity check
assert poly1305_normal(r,s,C1) % 2**128== T1
assert poly1305_normal(r,s,C2) % 2**128 == T2


ks1 = xor(ciphertext1,pt1)

goal = "But it's only secure if used correctly!"
goal=goal.encode()
ct_goal = xor(ks1[:len(goal)],goal)
C3 = padding(ct_goal,b'')

tag = poly1305_normal(r,s,C3)
tag = (tag % (1 << 128)).to_bytes(16,'little')
CT = ct_goal + tag + nonce1
io.sendline(CT.hex())
io.interactive()
#picoCTF{7urn_17_84ck_n0w_77243c82}

References

1. ChaCha20 and Poly1305 for IETF Protocols
   • Introduction to ChaCha20 and Poly1305.